Peering Equilibrium MultiPath or PEMP is a routing coordination framework that allows neighboring autonomous systems (ASes) to jointly control the flows of traffic between them. Equipped with a lightweight coordination mechanism and a game theory-based routing algorithm provided by PEMP, peering domains could alleviate the adverse effect of selfish routing behaviors and control effectively the traffic load on peering links. The two inter-domain routing scenarios presented in Fig.1 show the major differences between BGP hot potato routing and PEMP equilibirium routing. Comparing with the standard BGP, PEMP takes a significant advantage of multiple peering links between domains. By sharing the load among paths, the amount of traffic on each selected path is reduced, and consequently the hot path is chilled.
Figure 1: BGP hot potato routing vs PEMP
The specific inter-domain routing issue between peering ASes targeted by PEMP can be seen as a coordinated routing problem – one variation of the canonical competitive routing problem – in which two nodes in competition coordinate on the load balancing over parallel links. In the literature, approaches can be classified as negotiation-based and game-theoretic. The former approaches target the conception of an inter-domain routing protocol supporting route proposal and acceptance/rejection signaling. However, the complexity arisen in the negotiation processes limits the applicability of these solutions. In the latter approaches, peers use in-band signaling channel to exchange coordination information and make routing choice independently based on these information. Adopt this model, PEMP suggests an inter-domain routing strategy follows equilibrium profiles of a non-cooperative game built upon the exchanged routing costs.
PEMP is proposed as a solution to enhance routing stability and bilateral cost across inter-AS peering links. To be incrementally deployed by operators, instead of developing a novel routing coordination protocol, PEMP was designed with marginal modifications to BGP, the current Internet’s inter-domain routing protocol. The changes in BGP’s working processing to support equilibrium routing could be brieftly described as follows:
- BGP signaling: in the legacy BGP, the Multi-Exit Discriminator (MED) attribute can be used by one AS to suggest to a neighboring AS – connected via multiple interconnection points – an entry point to its own domain; the MED value is typically set to the interior gateway protocol routing cost toward the destination, so that it suggests a ranking over multiple inter-AS links for a given destination IP prefix. In PEMP, it is specified to use the MED as a coordination signaling media; it is coded to transport not only the incoming routing cost, but also the outgoing routing cost.
- BGP decision process: when multiple routes to a same destination via a same AS exist and are considered equivalent with respect to local preference and AS hop count, the least MED rule is used to route toward the downstream AS preferred exit point. With PEMP, the least MED rule is changed so that it decides the best route or the multiple routes that correspond to the equilibrium strategy profiles of the routing game between two ASes. The game components are built using the ingress/egress routing costs (four for each link) exchanged via the MEDs.
PEMP models the inter-AS bilateral routing decision process as a 2-player non cooperative game; the two ASes act as rational players – referred to as players I and II – and the game strategy sets – X and Y – are the available peering links toward a given destination IP network. A combination of choices forms a strategy profile (x, y) ∈ X × Y; every profile associates with a pair of unilateral payoff values that reflect the benefit of AS players associated with the corresponding routing decision. The payoff of each participant – f(x, y) and g(x, y), respectively – is a cost defined by the sum of directional unilateral cost components. For a given AS, the egress cost component – φI(x) and φII(y) respectively – depends on the strategy selected by the AS itself, while the ingress cost – ψI(y) and ψII(x) – is determined by the choice of its neighbor. Hence f(x, y) = φI(x) + ψI(y) and g(x, y) = φII(y) + ψII(x)
Therefore, the resulting game G(X, Y; f, g) is such that a profile indicates a link to use for each of the two players, for each of the two traffic flows from one network to the other. The two flows are considered to be equivalent, where equivalence may not strictly mean the same bit-rate, but also uneven bitrates (as it happens in content provider to transit provider peering agreements) and even a more generic equivalence definition. This implies that at least two distinct destination IP prefixes are associated to a routing game (one for each AS), and that at most each AS associates a set of IP prefixes to the routing game. The way to segment different routing games decisions can rely on the usage of the ‘BGP community’ marking, which can be captured by the BGP decision process. Under complete information sharing, both ASes can compute the same equilibrium solution. G(X, Y; f, g) is a potential game, i.e., each profile (x, y) can be associated with a potential value P(x, y) such that the difference in potential values between two profiles differing from an unilateral strategy move is the same independently of the other player strategy, i.e.
P(x, y) − P(x0, y) = P(x, y0) − P(x0, y0), ∀x,x0 ∈ X, ∀y,y0 ∈ Y.
In potential games, the minimum potential profile corresponds to a Nash equilibrium and always exists. Moreover, as proven in [1], for G all Nash equilibria always correspond to a potential minimum, which is not true for the general case. This property makes PEMP routing attractive toward realistic implementations.
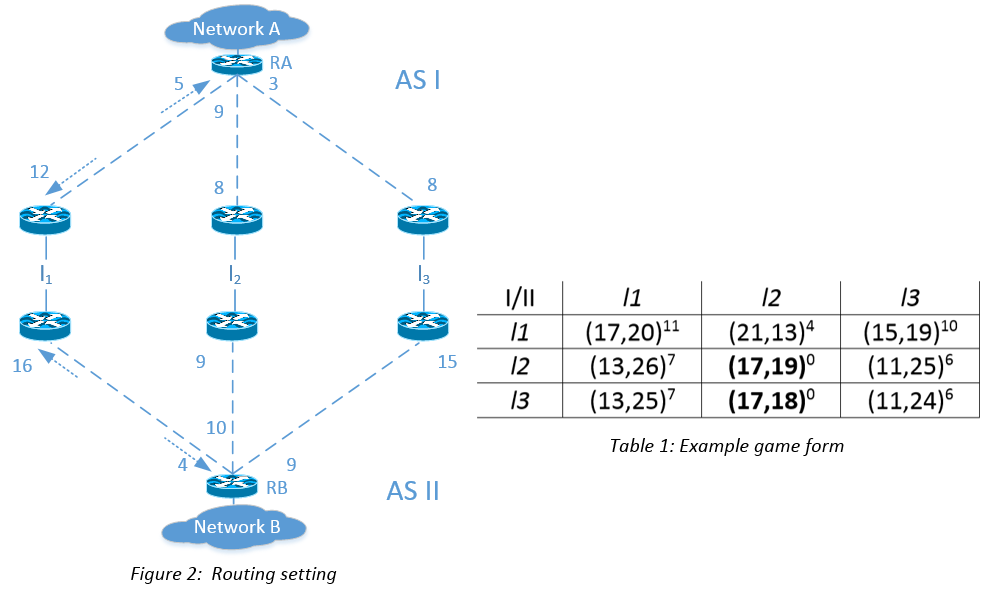
An example is given in Fig. 2. AS I and AS II interconnect with each other via three peering links: l1, l2 and l3. As a result, router RA in AS I has three options for routing traffic from source network A to destination network B. Similarly, the same set of strategy is also available at router RB in AS II. For each intra-domain path connecting customer’s network with border router, there are two internal routing costs: (a) an ingress cost represents the payoff when incoming traffic from peering AS flows on that path and (b) an egress cost indicates the payoff when forwarding packets to peer via that path. The corresponding game form is given in Table I: it summarizes all the possible outcomes of the routing game built from the above topology, it also includes the payoff and potential value of each profile. For instance, profile (l3,l2) has a payoff value of (17, 18) in which 17 is the sum of 8 and 9, that are, respectively, the routing costs at AS I when routing outgoing traffic via l3 and receiving incoming traffic from l2. According to property of potential game, both profiles (l2,l2) and (l3,l2) are in the Nash set. When there are multiple equilibria, if there exists a Pareto-superior one, it can be preferred as an implicit coordination rule of thumb. Otherwise, in general, load-balancing can be performed on the equlibrium profiles. In that specific example, profile (l3,l2) is Pareto-superior to (l2,l2), so only (l3,l2) is selected, which implies that packets from A to B are sent through link l3, while traffic flow on the reverse direction are routed on link l2.
It is worth noting that, in the provided example, the routing outcome is the same as early exit (hot potato) routing, which shows that the provided framework is correctly modeling the current interconnection policies; more generally, this situation manifests when multiple profiles with the same minimum potential exists. Relying on the IGP routing cost to make routing decisions, PEMP faces the same challenge of routing instability when transient failure occurs in the intra-domain network that legacy BGP routing faces. PEMP circumvents this problem by taking into account the IGP path cost variation when deciding which profiles can eventually be considered in the routing equilibrium solution. A profile (x, y) is selected when it has potential within the minimum potential plus a threshold τ whose value is derived from the IGP path cost variation due to intra-AS link failures. Indeed, whenever a link failure happens, the costs for routing traffic across selected paths can increase. Consequently, the potential values P(x, y) are recalculated, and new routing decision is made to adapt with such path cost deviation. By determining a proper threshold τ, the network operator can anticipate routing variations caused by transient failures and hence select robust equilibrium routing solutions.
REFERENCE
[1] Stefano Secci et al, “Peering Equilibrium Multipath Routing: A Game Theory Framework for Internet Peering Settlements“, IEEE/ACM Transactions on Networking, Vol. 19, No. 2, pp: 419-432, April 2011.

